Comparing of several Group Means by One-Way ANOVA using SPSS
In a previous post entitled "One-Sample T-Test in Chemical Analysis – Statistical Treatment of Analytical Data" the statistical tests presented were limited to situations in which there were only up to two levels of the independent variable (i.e. up to two experimental groups, two experimental conditions) and the data were normally distributed (histogram of normal distribution was obtained by plotting data). Methods were described for comparing two means to test whether they differ significantly. However, in analytical work there are often more than two means to be compared. Some situations encountered are:
- comparing the mean results for the concentration of an analyte by several different methods
- comparing the mean results obtained for the analysis of a sample by several different laboratories
- comparing the mean concentration of a solute A in solution for samples stored under different conditions
- comparing the mean results for the determination of an analyte from portions of a sample obtained at random (checking the purity of a sample)
Therefore, it is common in analytical work to run experiments in which there are three, four or even five levels of the independent variable (that can cause variation of the results in addition to random error of measurements) and in these cases the tests described in previous posts are inappropriate. Instead a technique called analysis of variance (ANOVA) is used. ANOVA is an extremely powerful statistical technique for analysis of data that has the advantage that it can be used to analyze situations in which there are several independent variables (or better several levels of the independent variable). In the examples given above levels of the independent variable are the different methods used, the different laboratories, the different conditions under which the solutions were stored.
The so called one-way ANOVA is presented in this post since there is one factor in addition to the random error of the measurements that causes variation of the results (methods, laboratories, storage conditions respectively). More complex situations in which there are two or more factors (i.e methods and laboratories, methods and storage conditions), possibly interacting with each other are going to be presented in another post.
When the one-way ANOVA test should be used?
One-way ANOVA should be used when there is only one factor being considered and replicate data from changing the level of that factor are available. One-way ANOVA will answer the question: Is there a significant difference between the mean values (or levels), given that the means are calculated from a number of replicate measurements? It tests the hypothesis that all group means are equal. An ANOVA produces an F-statistic or F-ratio, which is similar to a t-test (t-statistic) in that it compares the amount of systematic variance in the data to the amount of unsystematic variance.
Why not use several t-tests instead of ANOVA?
Imagine a situation in which there were three experimental conditions (Method 1, Method 2 and Method 3) and we were interested in comparing differences in the means of the results of these three methods. If we were to carry out t-tests on every pair of methods, then we would have to carry out three separate tests: one to compare means of Method 1 and 2, one to compare means of Method 1 and 3 and one of Method 2 and 3. Not only is this a lot of work but the chance of reaching a wrong conclusion increases. The correct way to analyse this sort of data is to use one-way ANOVA.
Results from statistical analysis have a certain value only if all relevant assumptions are met. For a one-way ANOVA these are:
- Normality: The dependent variable is normally distributed within each population (ANOVA is a parametric test based on the normal distribution). Since most of the time we do not have a large amount of data it is difficult to prove any departure from normality. It has been shown, however, that even quite large deviations from normality do not affect the ANOVA test. ANOVA is a robust method with respect to violations of normality. If there is a large amount of data tests for normality can be used such as the Normal Q-Q plots, the Shapiro-Wilk test of normality, plotting histograms and skewness and kurtosis.
- Homoscedasticity: The variance (spread) between groups (populations) is homogeneous (all populations have the same variance). If this is not the case (this happens often in chemical analysis) then the F-test can suggest a statistically significant difference where none is present. The best way to check for this is to plot the data. There are also a number of tests for heteroscedasity like Bartlett's test and Levene's test. Homoscedasticity not holding is less serious when the sample sizes are equal. It may be also overcome this type of problem in the data by transforming it by taking for example logarithms (logs)
- Independent data: This often holds if each case (row of cells) represents a unique observation
If assumptions 1 and 2 seem seriously violated then the Kruskal-Wallis test can be used instead of ANOVA. This test is a non-parametric test and therefore does not require normally distributed data.
The principle of the one-way ANOVA test is more easily understood by means of the following example.
Example I.1
Figure I.1 shows the analytical results obtained regarding the weight of Au (in grams/ton) in a certified reference material X. Three different methods (Method 1, 2 and 3) were used for the determination and six replicate measurements were made in each case. Is there a significant difference in the means calculated by each method?

Before running an ANOVA test let us first plot our data using a histogram (frequency distribution curve). The results in Fig. I.1 have been inserted in an SPSS spreadsheet. In SPSS access the main dialog box using Graphs --------> Legacy Dialogs --------> Histogram
The following histogram is obtained (Fig. I.2). A split histogram gives information regarding the three assumptions mentioned above.

- Normality: All distributions look reasonably normal even though there is not a large amount of data. The dependent variable seems normally distributed within each population. It has been shown, however, that even quite large deviations from normality do not affect the ANOVA test.
- Homoscedasticity: The two histograms - first and third - are roughly equally wide. The second seems to be wider due to a outlier. It seems as though the results have roughly equal variances over the three methods. As a rule of thumb variances are unequal when the larger variance is more than 4 times the smaller variance. This is not the case in this example. Levene's test is going to be used to prove that variances for the three methods are equal in a formal way.
- Independent data: Data are independent since each case (row of cells) represents a unique observation
In SPSS access the main dialog box using Analyze --------> Compare Means --------> One-Way Anova (Fig. I.3) and select as Dependent List (variable): Analytical_Result_g and as Factor: Method. Press O.K. (Fig. I.4). The means of the analytical results obtained by Method 1, 2 and 3 (methods are a factor that may affect the means) are compared. The question that has to be answered is if the differences between these means are statistically significant or these mean values are the same.


The selection Options is pressed (Fig. I.4) and Descriptive Statistics, Homogeneity of Variance Test and Means Plot is checked in the one-way ANOVA SPSS dialog box and Continue is pressed (Fig. I.5).

After running the ANOVA test the following results are obtained (Fig. I.6):
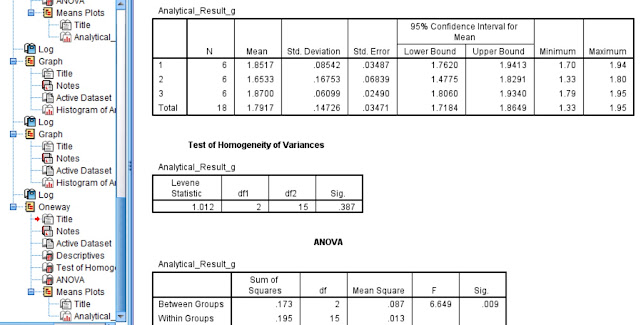
- A Descriptives table for the dependent variable Analytical_Result_g. Where N is the number of replicates by each method (N=6). The mean weights of Au are almost equal when Methods 1 and 3 were used - 1.85 and 1.87 respectively - and they differ from the mean of Method 2 which is 1.65. Our main research question is whether these means differ significantly for the three different methods.
- A table for the test of Homogeneity of Variances (Levene's test). It checks whether the variances of the results obtained by the three methods differ significantly. If p ‹ 0.05 then they differ significantly. In this case p = 0.387 › 0.05 and therefore the variances of the three means do not differ significantly. Therefore, the ANOVA test was the right choice.
- An ANOVA table. Where the degrees of freedom df for Between Groups and Within Groups are given (2 and 15 respectively) and the F statistic F= 6.649. The p value denoted by Sig = 0.009 ‹ 0.05 indicates that the three means differ significantly due to the different analytical methods.
Relevant Posts
Statistics – Frequency Distributions, Normal Distribution, z-scores
Testing for Normality of Distribution (the Kolmogorov-Smirnov test)
References
- D.B. Hibbert, J.J. Gooding, "Data Analysis for Chemistry", Oxford Univ. Press, 2005
- J.C. Miller and J.N Miller, “Statistics for Analytical Chemistry”, Ellis Horwood Prentice Hall, 2008
- Steven S. Zumdahl, “Chemical Principles” 6th Edition, Houghton Mifflin Company, 2009
- D. Harvey, “Modern Analytical Chemistry”, McGraw-Hill Companies Inc., 2000
- R.D. Brown, “Introduction to Chemical Analysis”, McGraw-Hill Companies Inc, 1982
- S.L.R. Ellison, V.J. Barwick, T.J.D. Farrant, “Practical Statistics for the Analytical Scientist”, 2nd Edition, Royal Society of Chemistry, 2009
- A. Field, “Discovering Statistics using SPSS” , Sage Publications Ltd., 2005
Key Terms
comparing several means, analysis of variance, ANOVA, t-tests,
No comments:
Post a Comment