Solving Weak Acid and Weak Base pH problems
Solving Weak Acid and Weak Base pH problems
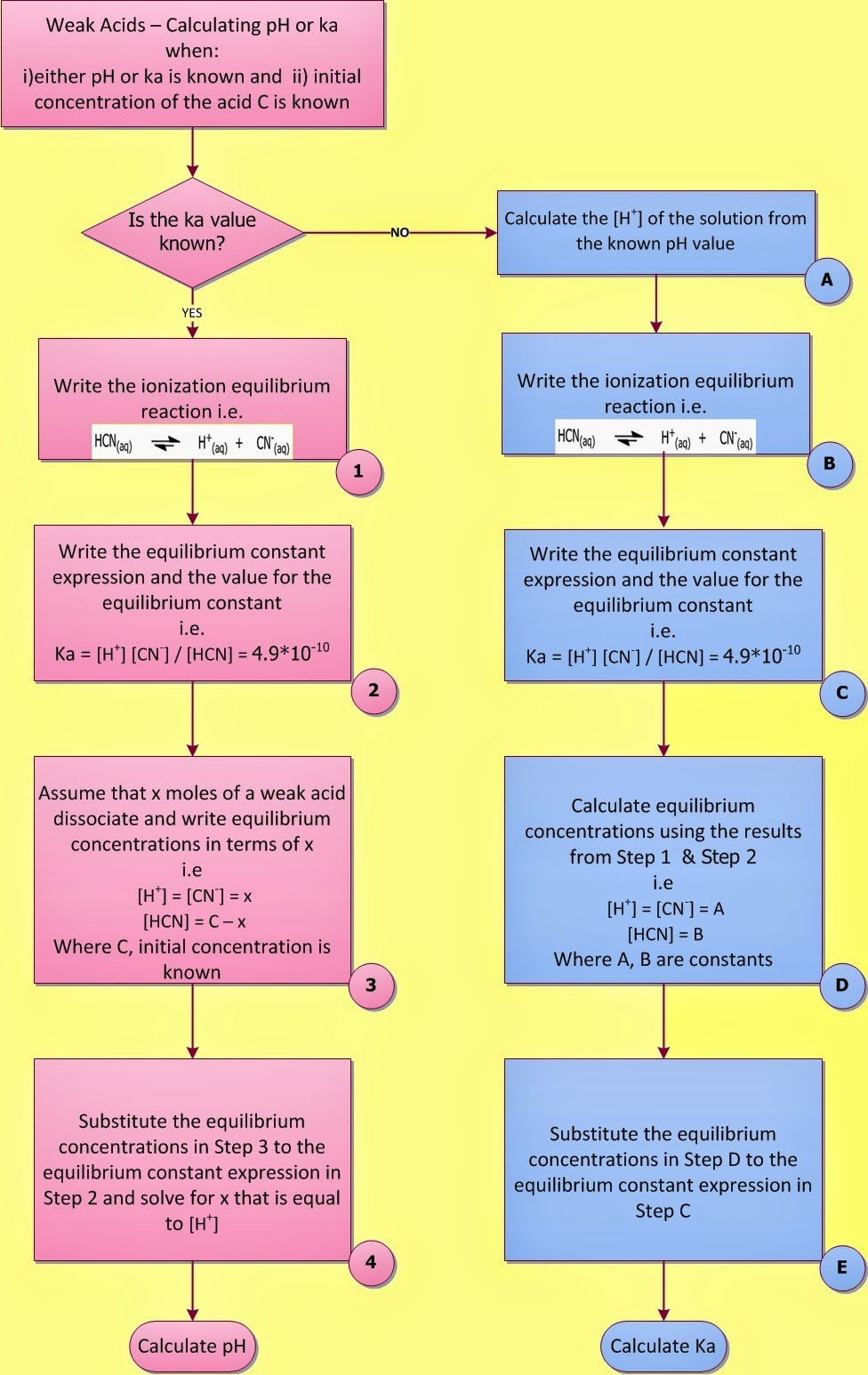 |
| Fig. I.1: Calculating the pH of a weak acid |
Some extra solved examples on weak acid (base) chemistry are shown below. The “chemical
approach” method is used for the solution.
Example I.1
What the concentration of
an acidic solution ΗΑ must be so
that
[H+]= 3.5 * 10-4 M (ka =1,7 * 10-5)
STEP
|
RESULT
|
|
GIVEN
|
[H+]= 3.5 * 10-4 M
ka =1.7 * 10-5
|
UNKNOWN
|
[HΑ] = ;
|
|
I
|
HA is a weak acid as the ka value shows.
Write the ionization
equilibrium reaction:
HΑ  Η+ +
Α- (1) Η+ +
Α- (1)
|
II
|
Write down the
equilibrium constant expression and the equilibrium constant:
ka = [Η+]
. [A-] / [HA] = 1.7 * 10-5 (2)
|
III
|
Let
us suppose that y M is the initial concentration of HA. Then the equilibrium
concentrations of the species involved are as follows:
Initial
|
y Μ
|
0 Μ
|
0 Μ
|
Change
|
-3.5 * 10-4
|
+3.5 * 10-4
|
+3.5 * 10-4
|
Final
(at
equilibrium)
|
(y – 3.5 * 10-4)
|
3.5 * 10-4
|
3.5 * 10-4
|
|
IV
|
From (2) and the equilibrium
concentrations from the above table:
ka = [Η+] . [A-] / [HA] = (3.5 * 10-4)2 / (y-3.5
* 10-4) = 1.7 * 10-5
and y = 7.2 *
10-3 M
Therefore [HΑ]
= 7.2 * 10-3 M
|
Example I.2
A weak acid solution is prepared by
dissolving 8.3 * 10-1 g of HA in water. The final volume of the solution is measured to be 100 ml. What is the equilibrium
concentration of the species involved? (kΗΑ = 1.8 * 10-4, ΜΒΗΑ = 46 g/mol).
STEP
|
RESULTS
|
|
DATA
|
mHA =
8.3 * 10-1 g
VΔ =
100 ml
kHA = 1.8
* 10-4
ΜΒΗΑ = 46 g/mol
|
UNKNOWN
|
[HΑ] = ? [Η+]
= ?
[A-] = ?
|
|
|
|
I
|
HA is a weak acid as we can see from kHA. Therefore,
it dissociates partially in water.
Write the ionization equilibrium reaction:
HΑ
 Η+ +
Α- (1) Η+ +
Α- (1)
Calculate the moles
of ΗΑ in
solution:
nHA = 8.3 *
10-1 g /46 g/mol = 1.8 * 10-2 mol
The initial
concentration of ΗΑ is calculated as
follows:
100 ml
solution contain 1,8 . 10-2 mol ΗΑ
1000 ml
solution
contain y
= ; mol ΗΑ
y = [HΑ]initial =1.8 * 10-1
mol/ℓ
(2)
|
II
|
Write down the equilibrium constant expression and
the equilibrium constant:
kHA = [Η+]
. [A-] / [HA] = 1,8 . 10-4 (3)
|
III
|
Let us suppose that x moles ΗΑ dissociate.
The equilibrium concentration of the
species involved is given below:
|
HΑ
|
Η+
|
Α-
|
Initial
|
0.18 Μ
|
0
|
0
|
Change
|
-x M
|
+x M
|
+x M
|
Final (at equilibrium)
(στην χημ.
ισορρ.)
|
(0.18-x) M
|
+x M
|
+x M
|
|
IV
|
From (3) and the equilibrium concentrations
of the species involved:
ka = [Η+] . [A-]
/ [HA] = (x)2 / (0,18-x ) =
1.8 * 10-4
(x)2
/0.18 = 1.8 * 10-4
x = 5.7 * 10-3 M (4)
(assuming that 0,18-x ≈ 0,18
since ΗΑ is a weak acid and it partially
dissociates in water. Therefore the value of x
will
be small compared to the initial concentration of ΗΑ)
Checking for the validity of the above
approximation: If the value of x is less than 5% of the initial concentration
of HA the approximation 0,18-x ≈ 0,18
is valid.
5.7 * 10-3 * 100 /
0.18 = 3.2%
|
Example I.3
The ionization constant
of NH3 in water is 10-5. Calculate the following for a 0.1 M NH3 solution: a) the degree of dissociation α b) the concentration of [OH-] in solution
STEP
|
RESULTS
|
|
DATA
|
ΝΗ3
kb
= 10-5
[ΝΗ3]
= 0.1 M
|
UNKNOWNS
|
α = ? [ΟΗ-] = ?
|
|
|
|
I
|
ΝΗ3 is a weak base as the value
of kb shows. Therefore, it dissociates partially in water
according to:
H2O +
ΝΗ3  ΝΗ4+ +
ΟΗ- (1) ΝΗ4+ +
ΟΗ- (1)
Let us suppose that α
is the degree of dissociation of ΝΗ3 in water. Therefore:
α = moles ΝΗ3 that dissociate /
total moles ΝΗ3
Therefore moles ΝΗ3 that
dissociate = 0.1 * α (2)
|
II
|
Write down the equilibrium constant expression and
the equilibrium constant:
kb = [NΗ4+] . [OH-]
/ [NH3] = 10-5
(3)
|
III
|
The equilibrium
concentration of the species involved is given below:
|
ΝΗ3
|
ΝΗ4+
|
ΟΗ-
|
Initial
|
0.1 Μ
|
0
|
0
|
Change
|
(0.1-0.1α) M
|
+0.1 * α M
|
+0.1 * α M
|
Final
(at equilibrium)
|
0.1 * (1-α) M
|
0.1 * α M
|
+0.1 * α M
|
|
IV
|
From (3) and the above equilibrium concentrations of the
species involved:
Kb
= (0.1 * α). (0.1 * α) / 0.1 * (1-α) = 10-5 = 0.01 * α2
/ 0.1 = 10-5
Therefore,
α = 0,01 (4)
Assuming
that (1-α) ≈ 1 since the value of α
is small compared to [ΝΗ3] = 0.1 M
Therefore [OH-] = 0.1 *α = 0.1
* 0.01 = 10-3 M
Therefore
α = 0.01 and [OH-] = 10-3 M
|
Relevant Posts
References
J-L.
Burgot “Ionic Equilibria in Analytical Chemistry”, Springer Science &
Business Media, 2012
J.N.
Butler “Ionic Equilibrium – Solubility
and pH calculations”, Wiley – Interscience, 1998
Clayden,
Greeves, Waren and Wothers “Organic Chemistry”, Oxford,
D.
Harvey, “Modern Analytical Chemistry”,
McGraw-Hill Companies Inc., 2000
Toratane
Munegumi, World J. of Chem. Education, 1.1, 12-16 (2013)
J.N.
Spencer et al., “Chemistry structure and dynamics”, 5th Edition, John Wiley
& Sons, Inc., 2012
L.
Cardellini, Chem. Educ. Res. Pract. Eur., 1, 151-160, (2000)



