Weak Acids and Bases – Calculate the pH of a weak acid (a general equation)
The weak acid (base) general equation
Let us now find a general equation
for the pH of a weak acid HA (or for [H+]). This is the mathematical
approach.
Mathematical Approach:
There are two equilibria present: i) the dissociation of water and ii) the dissociation of the weak acid ka
[H+]
[OH-] =
kw (1)
[H+]
[A-] =
ka [HA] (2)
If the concentration of the acid in
solution is C (M, moles/l), a mass balance on the anion A gives:
C = [HA] +
[A-]
(3)
and a charge balance gives:
[H+] = [OH-] +
[A-]
(4)
Let us assume that ka,
kw and C are known. Then there are four
equations and four unknowns (shown in red in equations (1) to (4)).
A general expression for
[H+] (or for the pH of a weak acid) in this case would be an expression
in terms of the known ka, kw and C. Therefore, the unknowns have to be eliminated starting
from [HA] or [OH-]
that are contained in the least number of equations.
Let us eliminate first [OH-]. Solving equation (1) for [OH-] and substituting it in equation (4):
[H+]
[OH-] =
kw and [OH-] = kw /
[H+] (1’)
By substituting (1’) to (4)
eliminates [OH-]:
[H+] = [OH-] +
[A-] = kw / [H+] + [A-] (5)
Next let us eliminate [HA] by solving equation (3) for [HA] and
substituting in equation (2):
C = [HA] +
[A-] and
[HA] = C - [A-]
(3’)
Substitute (3’) in equation
(2) and eliminate [HA]:
[H+]
[A-] =
ka [HA] =
ka (C - [A-]) (6)
Now let us eliminate [A-] by solving equation (5) for [A-] and substitute in equation (6):
[H+] = kw / [H+] + [A-] and [A-] = [H+] -
kw / [H+] (7)
Substituting (7) in equation
(6):
[H+]
[A-] =
ka [HA] =
ka (C - [A-]) and
[H+] ([H+]
- kw /
[H+]) =
ka (C -[H+] - kw /
[H+]) ) (8)
Rearranging (8) we get a cubic
equation in [H+]:
[H+]3 + ka[H+]2 – (kw + ka C) [H+] - kw ka = 0 (9)
Using the known values of C,
ka, kw equation (9) can be
solved for [H+] and the pH can be calculated. The solution of the cubic
equation is straightforward but tedious.
In our days, solution of equations
like (9) has become easier by using on line cubic calculators.
Example I.1
Calculate the pH of a 0.20 M solution of HCN (ka = 4.9*10-10)
Data
|
[HCN]= C = 0.20 M
ka =
4.9*10-10
|
Unknown
|
pH = ?
|
The ka indicates that HCN
is a weak acid. It dissociates partially in water according to:
 |
By following the above mathematical
treatment (exact solution) equation (9) becomes:
Solutions to equations like the
above cubic equation are given by on-line cubic calculators (Fig. I.1):
![Fig. I.1: Three solutions to the above cubic equation are given by the Wolfram/Alpha calculator. The positive solution is the one with any physical meaning. Therefore [H+] = 9.9 * 10-6 M. Fig. I.1: Three solutions to the above cubic equation are given by the Wolfram/Alpha calculator. The positive solution is the one with any physical meaning. Therefore [H+] = 9.9 * 10-6 M.](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhVJnTtr4QtW8QWMKH3IN4wF_lV54dsXOA6bU_-mjX4yxvwIzy7FcYFvapZOcyHUcryVT_VaKF5RtTXCdMmTqECTBqT2pB3cAxArsmPMCA4p-L8NHdbqRT9HeemJyY8T7vJcTYF3s0bc1I/s1600/cubic1_r.png) |
|
Fig. I.1: Three solutions
to the above cubic equation are given by the Wolfram/Alpha calculator. The
positive solution is the one with any physical meaning. Therefore
[H+] = 9.9 * 10-6 M.
|
Therefore [H+] = 9.9 * 10-6 M and the pH
of the solution can be calculated:
pH = -log[H+] = -log (9.9
* 10-6) = 5.0
Approximations on the Equation giving [H+] for weak
acids
The error of equilibrium data are
usually ± 5% so it is usually possible to make a number of approximations on
equation (9) greatly simplifying the solution of problems like the one given in
Example I.1:
Case 1
If the acid is not extremely weak or
the solution very dilute, the concentration of [OH-] can be neglected in
comparison to that of [H+] since [OH-] <<<
[H+]. Therefore:
[H+] ([H+] -
kw / [H+]) = ka (C
-[H+] - kw / [H+]) ) (8)
[H+] ([H+] -
kw / [H+]) = ka (C -[H+] -
kw / [H+]) ) ⇒ [H+] ([H+] - [OH-]) = ka (C
-[H+] - [OH-] ) ⇒ [H+] [H+] = ka (C
-[H+]) ⇒
ka =
[H+]2 / C -[H+] (8a)
Equation (8a) is a quadratic
equation:
[H+]2 +
ka [H+] - ka C = 0 (8a)
Case 2
If the acid is fairly concentrated
(more than 10-3 M) a simplification can be achieved by making the
assumption that [H+] <<< C since the acid dissociates slightly
and very little [H+] is produced. Therefore equation (8a) reduces
to:
ka =
[H+]2 / C
⇒ [H+] ≈ (ka C)1/2 (8b)
As a general rule:
Several approximations can be made
on the mass and charge balances by neglecting a concentration when it is added to
another.
The approximate system of equations
is solved
The results are checked for
consistency with the approximations
In the final form, all
approximations should introduce an error of no more than 5
If all the above show that the
approximations are not appropriate the equation must be solved in its exact
form.
Calculating ka from pH or pH from ka
In order to calculate either the ka for a weak acid (ka value) when the pH of its solution is known or the pH of a weak acid when the ka value is known the following procedure is followed (Fig. I.2):
Let’s try to solve now the
problem in Example I.1 using the above step-by-step approach – let’s
call it chemical approach - and compare with the mathematical approach previously
used. The drawback of using the mathematical approach is that formulas have to be
memorized that may lead to significant errors since they only give correct results
when certain assumptions are fulfilled.
Chemical Approach:
Example I.1 (continued…)
Calculate the pH of
a 0.20 M solution of HCN (ka = 4.9*10-10)
Given
|
[HCN]= C = 0.20 M
ka =
4.9*10-10
|
Asked for
|
pH = ?
|
Step 1: Write the ionization
equilibrium reaction
 |
Step 2: Write the equilibrium
constant expression and the value for the equilibrium constant.
ka = [H+]
[CN-] / [HCN] = 4.9*10-10
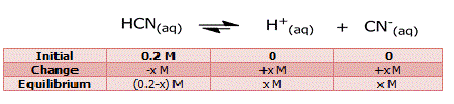
Step 3: Assume that x moles/l of HCN
dissociate. Then the concentrations of the species
involved in the equilibrium are:
ka = [H+]
[CN-] / [HCN] = (x)*(x) / (0.2-x) = 4.9*10-10 (9) ⇒
x2-4.9*10-10x+9.8*10-11 = 0
This expression leads to a quadratic
equation in x, which can be solved using the quadratic formula or a
calculator.
However, since the value of
ka is very small we can assume that x is small and so:
(0.2-x) ≈ 0.2 (10)
Then from (9) and (10): x2 / 0.2 = 4.9*10-10 and x = [H+] =
9.9*10-6
The value for x is exactly the same
with the one calculated using the mathematical approach. Therefore our assumption
(0.2-x) ≈ 0.2 is correct.
Therefore, pH = -log[H+]
= -log (9.9 * 10-6) = 5.0
Example I.2
Calculate the pH of a 0.3 M solution of acetic acid at
25 °C.
(ka= 1.8
* 10-5)
STEP
|
RESULT
|
NOTES
|
||||
|
Write down the given data
and the unknown.
|
|||||
I
|
Acetic
acid is a weak acid as the kα value shows and therefore it
dissociates partially in water.
Write down a relation
that connects given data and unknowns.
pH = -log [H+]
(1)
Write the ionization equilibrium
reaction:
CH3COOH
|
|||||
II
|
Write down the equilibrium constant expression and the
equilibrium constant:
ka
= [H+] [CH3COO-] /
[CH3COOH] =
1.8 * 10-5
(3)
|
|||||
III
|
Assume
that x mol /ℓ of acetic acid dissociate and write
down the equilibrium concentrations of the
species involved in terms of x.
|
||||||||||||||||
IV
|
By substituting in (3) the above equilibrium concentrations:
ka
= [H+] [CH3COO-] /
[CH3COOH]
= x
. x /(0.3-x) = 1,8 * 10-5
x2
/(0.3-x) = 1.8
*10-5
(4)
Equation
(4) is a quadratic equation in x that can be solved by
using a calculator or the well-known formula.
However, since acetic
acid is a weak acid and dissociates slightly in water and therefore x is
very small we can assume that 0,3-x ≈ 0,3
So (4)
becomes:
ka
= x .
x /0.3 = 1.8 *
10-5
x2 = (0.3)
(1.8 * 10-5)
x = 2.3 * 10-3 M
Therefore,
[Η+] = x = 2,3 *
10-3 M (5)
From (1)
and (5)
pH = -log [H+] =
-log
(2.3 *
10-3) =
2.64
|
For more solved weak acid and base problems please see the video and the links given below.
Relevant Posts
References
J-L. Burgot “Ionic
Equilibria in Analytical Chemistry”, Springer Science & Business
Media, 2012
J.N. Butler “Ionic Equilibrium – Solubility and pH
calculations”, Wiley – Interscience, 1998
D. Harvey, “Modern Analytical Chemistry”, McGraw-Hill
Companies Inc., 2000
Toratane Munegumi, World J. of
Chem. Education, 1.1, 12-16 (2013)
J.N. Spencer et al.,
“Chemistry structure and dynamics”, 5th Edition, John Wiley &
Sons, Inc., 2012
L. Cardellini, Chem. Educ. Res.
Pract. Eur., 1, 151-160, (2000)
Key Terms
pH weak acid solution, weak acids, bases, how to calculate pH, calculating pH, strong and weak acids bases, pH weak acid general equation, chemistry net, dissociation of water, dissociation of weak acid, calculating ka from pH, weak acid base pH calculation