Rates of Chemical Reactions and the Collision Model
Reaction rates are affected both by reactant concentrations and by temperature. The collision model, that is based on the kinetic-molecular theory, explains for both of these effects at the molecular level. In general only a small number of reactant collisions leads to products (in certain cases 1 in 1013 collisions).
The basic principles of the collision model (collision theory) are as follows:
- Molecules must collide to react – Collisions are necessary to transfer kinetic energy, to break reactant chemical bonds and form product bonds
- The greater the number of collisions per second the greater the reaction rate – This agrees with the observation that as reactant concentration increases the rate of a reaction increases since the number of collisions increases. It also agrees with the observation that as temperature increases molecular velocities also are increased and therefore collision frequency and reaction rate is increased
- Proper orientation of colliding molecules is essential for a reaction to occur – In most reactions, molecules must be oriented in a certain way during collision for a reaction to occur. The relative orientation of the molecules during collision facilitates bond formation between certain atoms (Fig I.1 and Fig. I.2)


-
Molecules must collide with enough energy (activation energy) for a reaction to occur – Upon collision the kinetic energy of the molecules is used to stretch, bend and finally break bonds leading to chemical reactions. Svante Arrhenius suggested that molecules must posses a minimum amount of energy for the reaction to occur that is called activation energy.
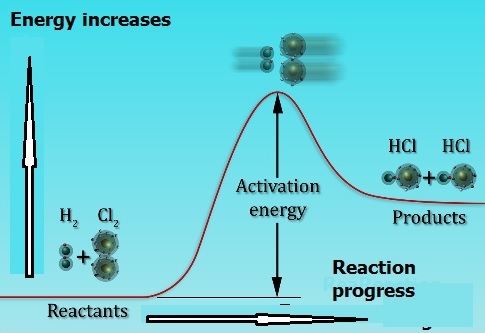
In general, the rate of a chemical reaction can be expressed as:
Rate of reaction = (number of collisions per unit time) * (fraction of reactants with sufficient energy) * (fraction of reactants with proper orientation)
The four above collision model principles are incorporated into the Arrhenius equation:
k = A * e-(Ea/RT) (Arrhenius equation) (1)
Where, k is the reaction rate constant
Ea is the activation energy
R is the gas constant (8.314 J/mol.K)
and T is the absolute temperature
A is the frequency factor, a constant related to the frequency of collisions and the probability that the collisions are favorably oriented
As the activation energy of a reaction increases the reaction rate constant k decreases because the fraction of the molecules that possess the required energy is smaller.
Determination of Activation Energy and the Arrhenius Equation
Using a Graph:
The activation energy Ea of a reaction can be calculated by taking the natural logarithm ln at both sides of the Arrhenius equation:
k = A * e-Ea/RT and lnk = ln(A * e-Ea/RT) and lnk = ln(A * e-Ea/RT) = lnA – Ea/RT
lnk = – Ea/RT + lnA (2)
y = mx + b (3)
Equation (2) has the form of the equation of a straight line (3). Therefore, a plot of lnk versus 1/T is a straight line with a slope m = – Ea/RT
The activation energy of the reaction can be determined experimentally by measuring k at a series of temperatures, plotting a graph of lnk versus 1/T and calculating Ea from the slope of the line.
Using a Non-Graphical method:
Equation (2) can also be used to calculate Ea if we know the rate constant of a reaction at two different temperatures.
Let us see the following example:
Example I.1
The rate constant of a reaction is k=2.52*10-5 at a temperature 189.7 °C. When the reaction temperature is 251.2 °C the rate constant of the reaction is k=3.16*10-3. Determine the activation energy Ea of the reaction.
By applying equation (2) twice at the following temperatures:
T1 = 273.15 + 189.7 = 462.85 K k1=2.52*10-5
T2 = 273.15 + 251.2 =524.35 K k2=3.16*10-3
lnk = – Ea/RT + lnA (2)
lnk1 = – Ea/RT1 (4) and
lnk2 = – Ea/RT2 (5)
By subtracting and rearranging (4) and (5) we get:
k1 = – Ea/RT1 (4) and
ln k1 / k2 = (Ea/R)(1/T2 – 1/T1) and
ln (2.52*10-5)/( 3.16*10-3) = (Ea/[8.314) * (1/524.35 – 1/462.85)] and
ln (2.52*10-5)/( 3.16*10-3) = [(Ea/8.314) * (-2.5*10-4)] and
ln (2.52*10-5)/( 3.16*10-3)] = [(-2.5*10-4) *Ea / 8.314] and
Ea = -4.83 * 8.314 /((-2.5*10-4) = 160626 J/mol = 160.6 kJ/mol
Relevant Posts - Relevant Videos
Rate of a Chemical Reaction - Chemical Kinetics
How to determine the order of a reaction by the initial rates method?
References
- J-L. Burgot “Ionic Equilibria in Analytical Chemistry”, Springer Science & Business Media, 2012
- J.N. Butler “Ionic Equilibrium – Solubility and pH calculations”, Wiley – Interscience, 1998
- Clayden, Greeves, Waren and Wothers “Organic Chemistry”, Oxford,
- D. Harvey, “Modern Analytical Chemistry”, McGraw-Hill Companies Inc., 2000
- J.N. Spencer et al., “Chemistry structure and dynamics”, 5th Edition, John Wiley & Sons, Inc., 2012 E. C. McGoran, J. Chem. Educ., 68, 19-23 (1991
Key Terms
reaction rates, reactant concentration, activation energy, collision model, collision theory
No comments:
Post a Comment